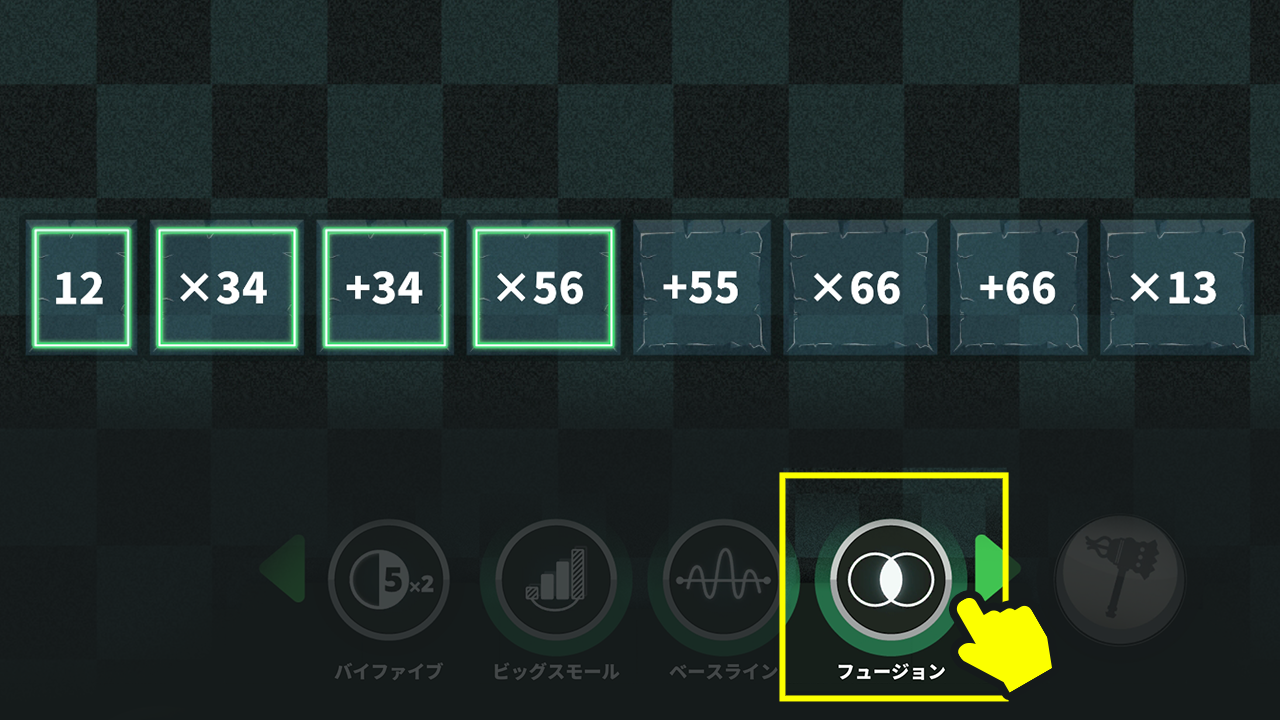
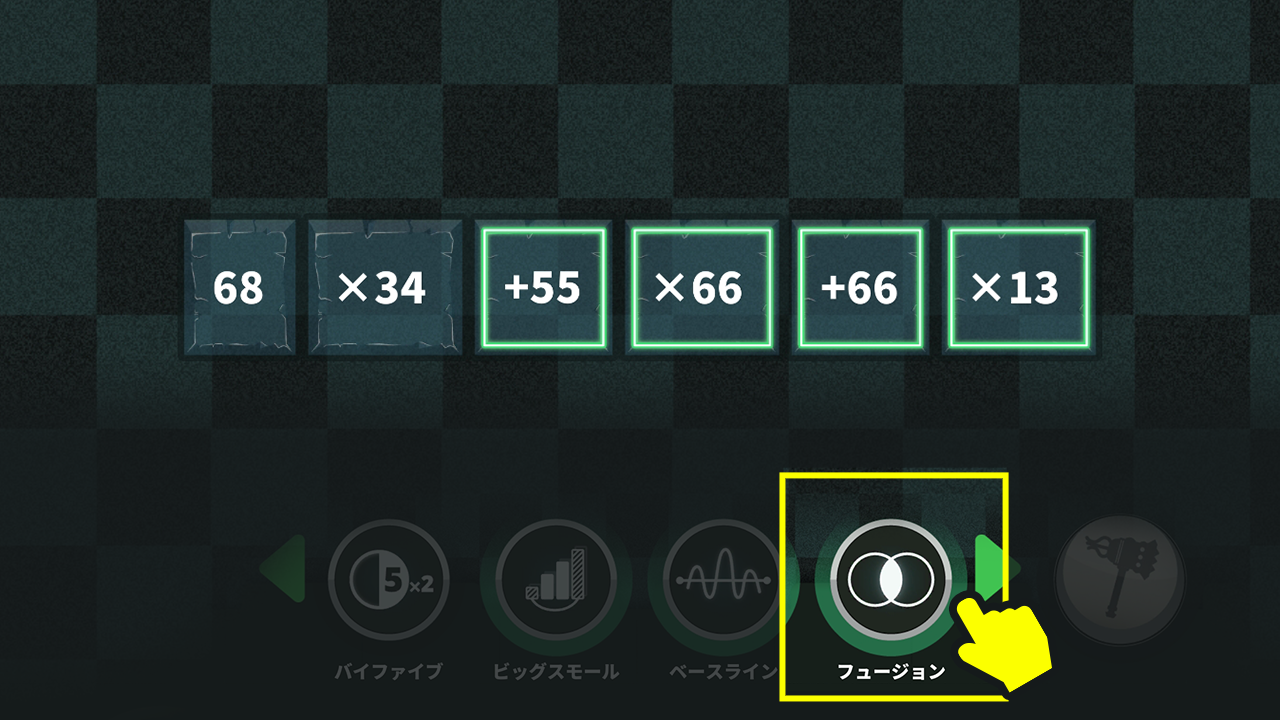
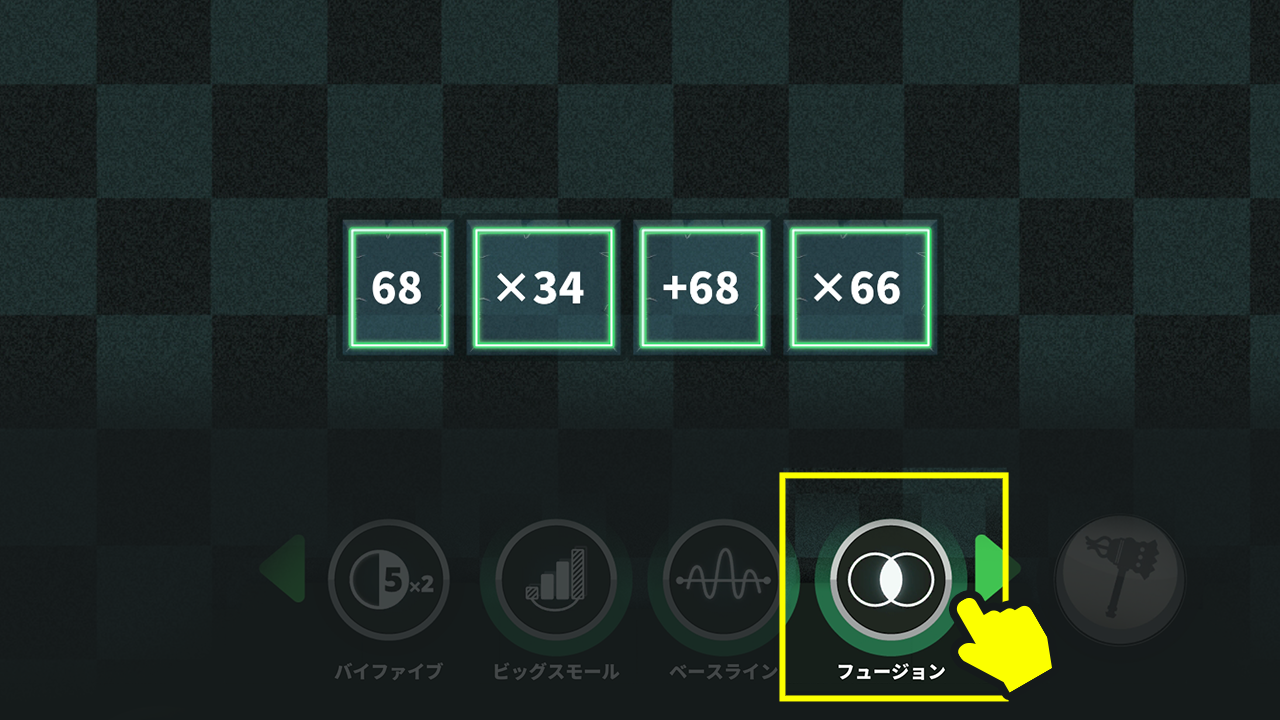
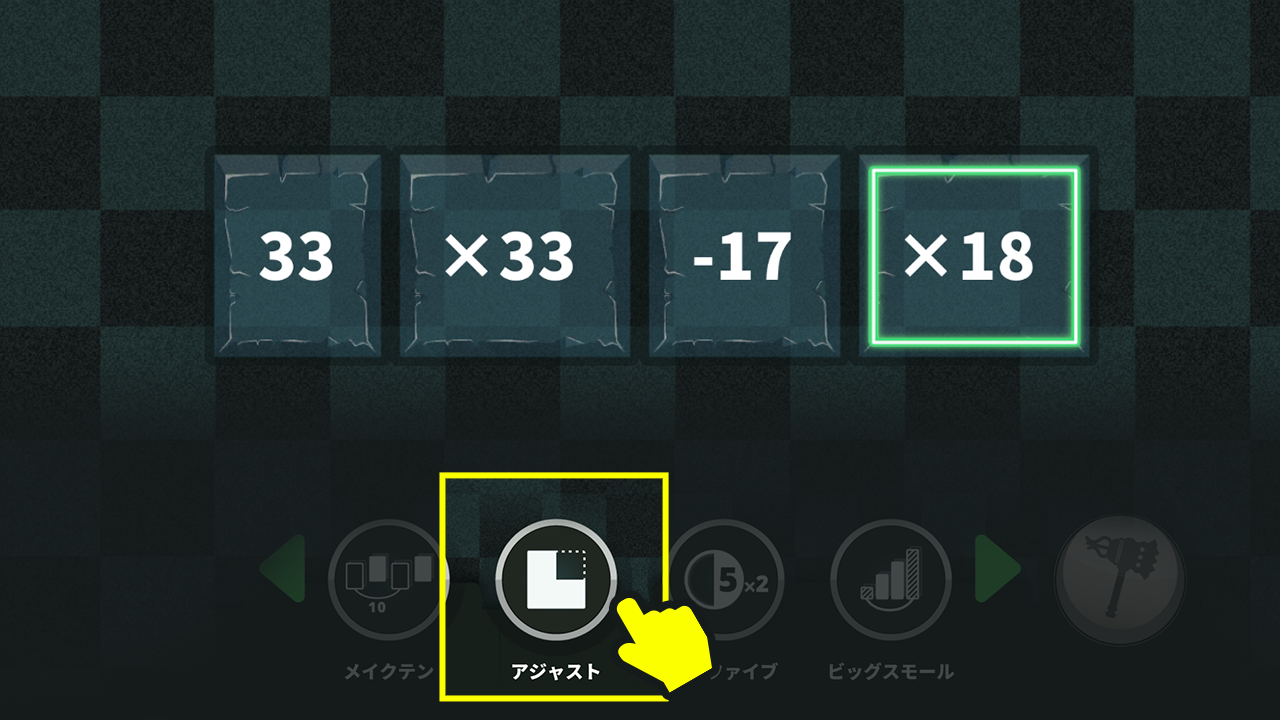
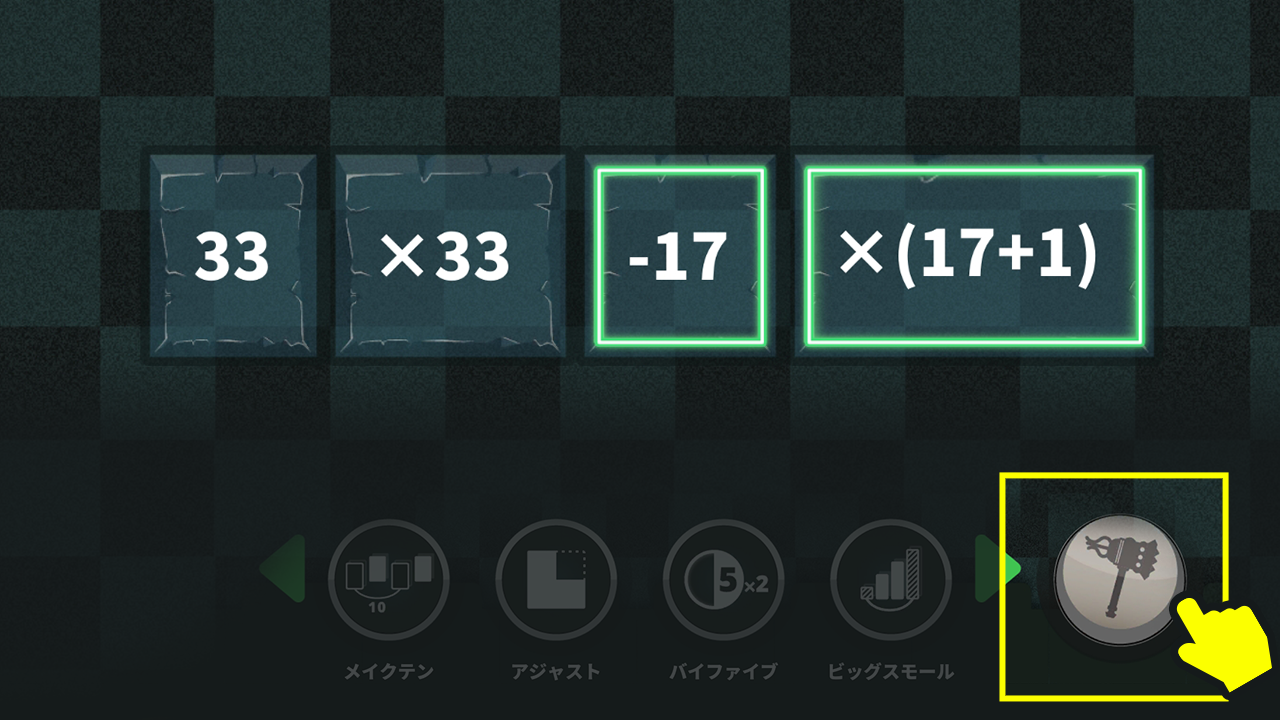
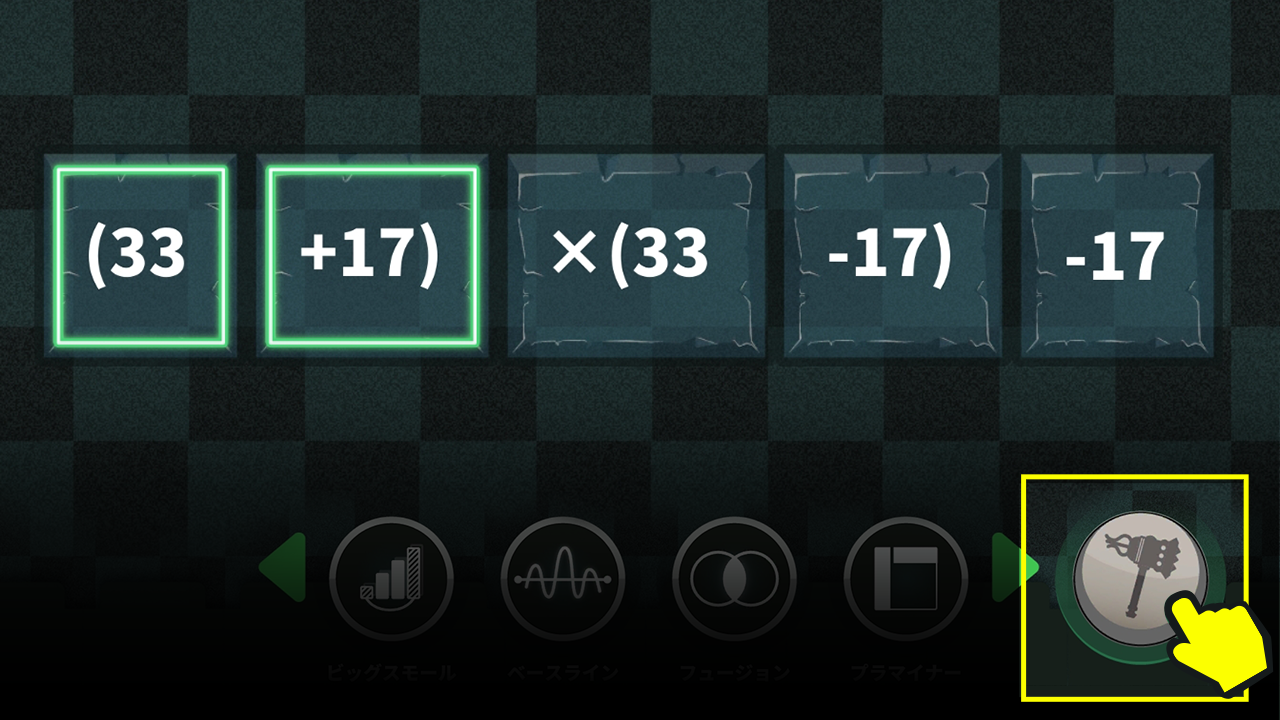
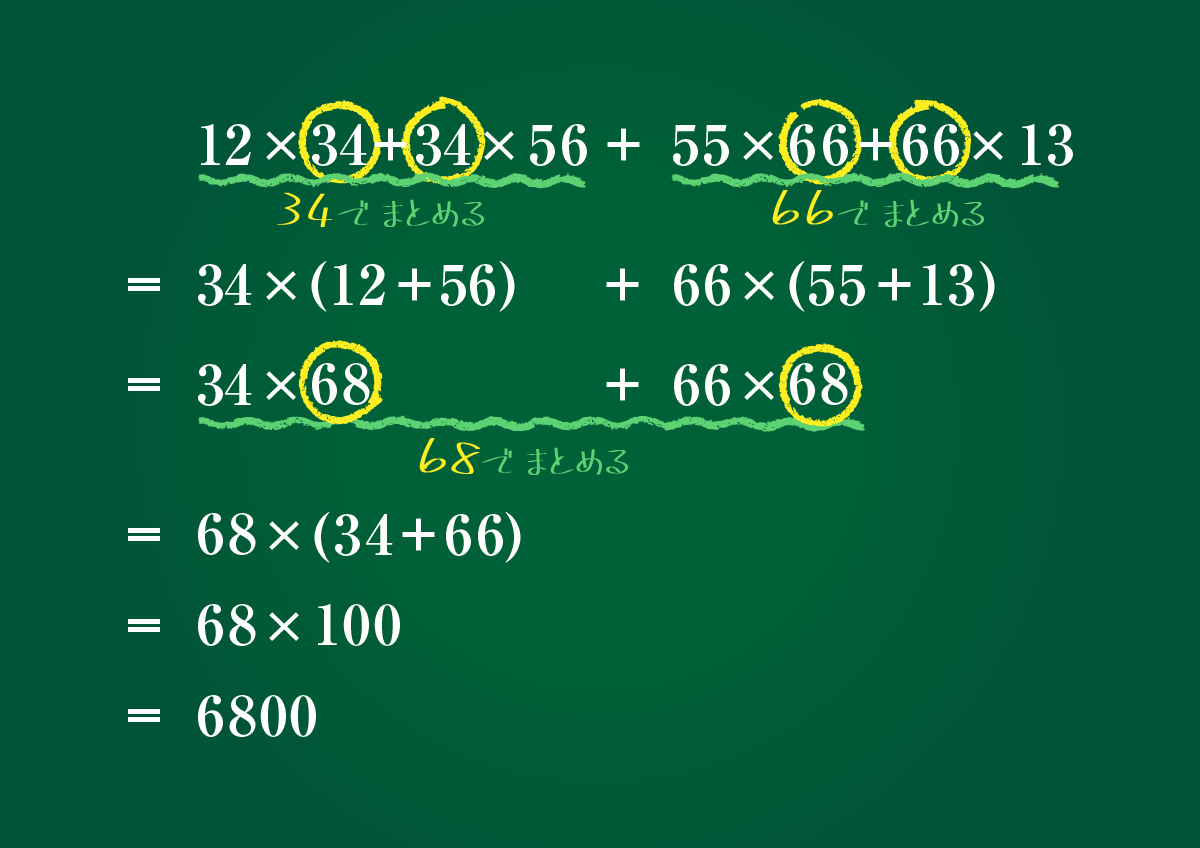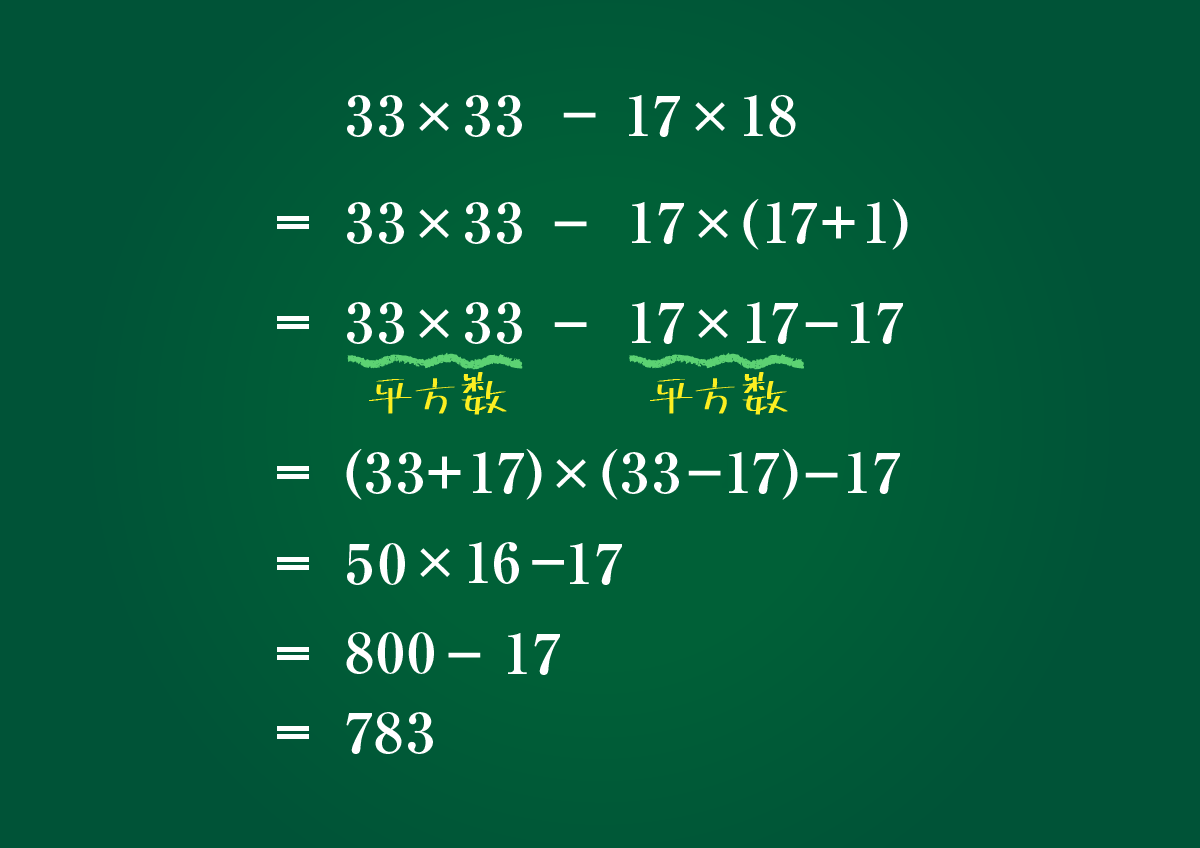$37×26+16×33+33×34+24×37$
$=37×(26+24)+33×(16+34)$
$=37×50+33×50$
$=(37+33)×50$
$=70×50$
$=3500$
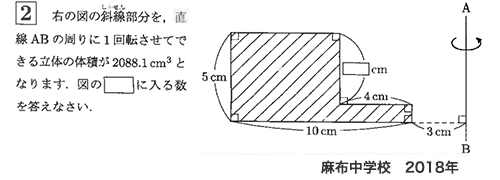
斜線部分を回転させてできる立体の体積は、
高さ□cmの部分と、高さ(5-□)cmの部分に分けて考えると、以下のように表せる。
$(13×13×3.14-7×7×3.14)×□+(13×13×3.14-3×3×3.14)×(5-□)$
$=(13×13-7×7)×3.14×□+(13×13-3×3)×3.14×(5-□)$
$=(13+7)×(13-7)×3.14×□+(13+3)×(13-3)×3.14×(5-□)$
$=20×6×3.14×□+16×10×3.14×(5-□)$
$=120×3.14×□+800×3.14-160×3.14×□$
$=800×3.14-40×3.14×□$
$=(800-40×□)×3.14$
この立体の体積は2088.1㎤なので、
$(800-40×□)×3.14=2088.1$
これを計算すると、
$□=3⅜$
工夫の技で、計算ミスを減らし時間を短縮!
中学入試の計算問題では、普通に解くと、一問の中で何度も計算する必要があるため、小さなミスが原因で不正解となってしまうケースが少なくありません。ミスを防ぐには、問題を解く段階で工夫することでキリの良い数字を作り、計算自体を出来る限り簡単にすることが大切です。暗算でも計算できる数字を意図的に作り出すことで、計算スピードも劇的に速くなりますし、検算の正確性も上がります。
工夫しようとする姿勢を身につけることが重要!
単なる反復学習では、その問題には対応できても、次第に応用が利かなくなり行き詰まってしまいます。常に工夫しようとする姿勢と、基本的な工夫の「技」が身についていれば、それをあらゆる局面で応用できるようになっていきます。
計算の工夫は、全ての学びの土台となる!
計算そのものは、中学受験に留まらず、その後の学習や、社会に出てからも必ず必要になるスキルです。数学で代数や定理などを用いるようになってからも、工夫する姿勢が身についているかどうかで、理解に大きな違いが生まれます。計算だけでなく、あらゆる未知の問題に直面した時に、「工夫しよう」と思えるかどうかは、結果を大きく左右するでしょう。
「究極の計算」
開発の経緯
計算は、算数・数学の基礎であり、誰もが生涯関わり続けていく、学問の根本となる分野です。単に解法や公式を覚える対処療法ではなく、計算を工夫したいと思って試行錯誤できるかどうかが、数学的思考全般の伸びを大きく左右します。
例えば、"$(x+y)×(x-y)$"のような問題。これを単に"$x^2-xy+xy-y^2$"と展開して計算するのでなく、「工夫してみよう」と試行錯誤することで、"$x^2-y^2$"という公式をより使いこなすことができるようになります。これで計算が楽になると、さらに他の問題でも工夫してみたいと思えるようになります。
テクノロジーが発達した現在では、教科学習を中心に、知識を効率的に吸収できる教育サービスが数多く生まれています。それにより教育がアップデートされる部分は大いにあるでしょう。
一方で、効率性や反復学習だけでは、本質的な理解や、学ぶ意欲につながりにくい面があると私たちは考えています。そこで、計算というテーマについても、「学ぶことの楽しさ」や「試行錯誤することの楽しさ」に焦点を当てて開発を続けてきました。
「究極の計算」は、単なる反復練習や公式の丸暗記でなく、試行錯誤しながら工夫することの楽しさを追求した末に生まれたアプリ教材です。計算が得意になる教材としてだけでなく工夫することの楽しさを感じられる教材として、中学受験をする・しないに関わらず、広く取り組んでいただければ幸いです。